Несколько простых опытов с 10-кг электронными весами на тензодатчиках

Оглавление

1. Введение
2. Весы и софт
3. Шумы ненагруженных весов
4. Чувствительность и задержки
5. Релаксация и гистерезис
6. Выводы
7. Дополнение

1. Введение

Несколько простых "прикидочных" экспериментов с тензовесами, которые будут описаны ниже, я делал исключительно для себя, ориентируясь на свои задачи. Но потом подумал, что эти результаты могут оказаться интересны еще кому-нибудь. Поэтому я решил оформить их в "презентабельном" виде и опубликовать здесь.

Электронные весы, имеющие какой-нибудь открытый интерфейс с компьютером - очень полезная штука в экспериментальном "хозяйстве". В Сети описано много разных вариантов их использования и в наших задачах. Меня они заинтересовали, в первую очередь, как датчик скорости отбора. В процессах автоматизированной ректификации такой датчик не очень-то и важен, т.к. отбор контролируется отдельным контроллером со специальным регулятором расхода продукта (электромагнитный клапан, перистальтический насос и т.п.). Обычно контроллер отбора не только регулирует скорость отбора, но и подсчитывает суммарный расход жидкости, прошедшей через устройство отбора. Тем не менее, возможны нештатные (аварийные) ситуации, которые контроллер устройства отбора отследить не в состоянии. Например, соринка заткнула жиклер клапана, окончательно износился и стал протекать кляп клапана, порвалась трубка перистальтического насоса и т.п. Для таких ситуаций в системе должен быть предусмотрен независимый датчик скорости отбора. Роль такого датчика как раз и могли бы выполнить электронные весы с компьютерным интерфейсом, которые сигнализировали бы систем о существенных отклонениях реальной скорости отбора от устанавливаемых контроллером отбора.

В этой задаче (создание "аварийного" датчика скорости отбора) есть упрощающие и усложняющие факторы. Упрощающими факторами является, во-первых, невысокая требуемая точность измерений. Во-вторых, при ректификации всегда отбирается почти чистый (точнее - неразбавленный) спирт с относительно небольшим содержанием других примесей. Поэтому никакой коррекции на плотность жидкости вводить не нужно. Т.е. измерение объема, с точностью до температурного фактора, эквивалентно измерению массы. Усложняющие факторы тоже есть. Во-первых, процессы ректификации обычно длительные (десятки часов), а скорости отбора относительно невелики (десятки мл/час при отборе голов и сотни мл/час при отборе других фракций). Т.е. дрейф весов под нагрузкой должен быть в разумных пределах. Во-вторых, тензодатчики должны длительное время "держать на себе" довольно приличный вес. Для средних ("бытовых":) кубов в 20-30 л это вес порядка 10-15 кг. А для второй ректификации он может быть еще больше. Точность весов с таким предельным весом, заявляемая производителем, обычно составляет величину порядка 1 гр. А поскольку скорость отбора - это производная веса по времени, то требования к точности весов и минимальным шумам становятся доминирующими и входят в серьезное противоречие с требованием большого предельного веса используемых весов.

Теоретически разбираться с этой дилеммой и глубоко влезать в метрологические проблемы тензовесов мне совсем не хотелось. Все-таки это лишь вспомогательное устройство в моей автоматике. Да и некогда. Поэтому я решил, что проще купить подходящие весы, переоборудовать их и проверить экспериментально годятся они для такой задачи или нет. При любом исходе, весы с компьютерным интерфейсом в хозяйстве никогда не помешают :)

2. Весы и софт

Про весы на ардуинках в Сети написано так много, что можно ограничиться лишь краткими комментариями по специфичным вопросам. В качестве основы я взял симпатичные и недорогие платформенные весы VT-8004 от фирмы Vitek. У них 4 сенсора, которые расположены на каждой из четырех ножек. Платформа стеклянная и круглая. Вполне устойчивая конструкция для 10-кг весов. Всю родную начинку (кроме, естественно, самих сенсоров) я выкинул и соединил сенсоры по мостовой схеме. Порывшись по сусекам, нашел платку с АЦП HX711, купленную давно для экспериментов с тензодатчиками. Простейший вариант для работы с АЦП и передачи данных в компьютер - любая ардуинка с нормальным USB. Из маленьких ардунок с USB у меня под рукой оказалась RF Nano. По сути это та же Arduino Nano, только с радиомодулем RF24L01 на борту. Радиомодуль для данной задачи не нужен, но другой ардуинки (с нормальным USB) под рукой не оказалось. Потом поставлю что-нибудь попроще. Все эти компоненты я соединил как положено и получил неплохие электронные USB-весы, вид которых показан на рисунках ниже.

Небольшой комментарий по поводу HX711. Этот АЦП может работать на двух частотах, определяемых уровнем линии RATE (15-я ножка микросхемы). При низком уровне на линии RATE частота работы АЦП составляет 10 Гц, при высоком уровне - 80 Гц. На многих платах с микросхемой HX711 эта ножка глухо посажена на землю. Т.е. по умолчанию установлена частота работы АЦП 10 Гц. Нам нужно 80. В этом случае 15-ю ножку микросхемы (линия RATE) нужно аккуратненько отпаять, отогнуть и соединить с соседней (c 16-й) ножкой тоненьким проводком. На 16-ю ножку на плате подается цифровое питание. После этого АЦП будет оцифровывать входной сигнал с частотой 80 Гц.

Теперь рассмотрим кратко программное обеспечение. В рассматриваемой системе есть два программируемых узла. Первый - плата Arduino, которая обеспечивает непосредственное взаимодействие с АЦП HX711, предварительную обработку и усреднение выборок АЦП (80 выборок в течение 1 сек). Второй программируемый узел - это компьютер (хост), который получает данные от ардуинки, производит (если нужно) дополнительную низкочастотную фильтрацию (усреднение) и обеспечивает интерфейс с пользователем. Это может быть любой компьютер с USB-портом. В принципе, это может быть и смартфон с USB. Я же использовал микрокомпьютер Raspberry Pi 4 (малинка) с HDMI монитором, беспроводной клавиатурой и мышкой. Можно работать и с "голой" малинкой по SSH с другого компьютера или телефона.  

Текст скетча для Arduino очень прост:

Скрытый текст

#include "HX711.h"

const int DOUT_PIN = 7;
const int SCK_PIN = 6;

HX711 scale;

void setup() {
  Serial.begin(57600);
  scale.begin(DOUT_PIN, SCK_PIN);
}

void loop() {
  if(scale.is_ready()) {
    long val = scale.read_average(80);
    Serial.println(val);
  }
}

Библиотеку для работы с АЦП HX711 можно скачать здесь. Для получения данных используется библиотечная функция read_average(80), в которой производится усреднение по 80 отсчетам АЦП за время приблизительно равное 1 сек. Т.е. хост получает от ардуинки приблизительно один отсчет в секунду. Этот отсчет уже усреднен в ардуинке по 80 отсчетам, полученным непосредственно от АЦП.

Программа для хоста написана на Python и приведена ниже:

Скрытый текст

import time
import serial
import curses
import numpy as np

ser = serial.Serial('/dev/ttyUSB0', 57600) # Поправить параметры, ежели что...

coef = 0.004165622 # Калибровочный коэффициент
offs = 370162 # Смещение
cgh = 3600.0*coef # Коэффициент для пересчета скорости отбора в г/час

tim = np.zeros(60) # Массив для хранения моментов времени отсчетов
codes1 = np.zeros(60) # Массив для хранения выборок АЦП, усредненных за 1 сек
codes10 = np.zeros(60) # Массив для хранения усредненных за 10 сек значений
codes30 = np.zeros(60) # Массив для хранения усредненных за 30 сек значений
codes60 = np.zeros(60) # Массив для хранения усредненных за 1 мин значений

stdscr = curses.initscr() # Основное окно curses
curses.curs_set(0) # Убираем изображение курсора
curses.noecho() # Убираем эхо при нажатии клавиш
curses.cbreak() # Убираем необходимость Enter для ввода с клавиатуры
stdscr.keypad(True) # Возможность ввода спецсимволов (PgUp, Left etc)
stdscr.nodelay(True) # Неблокирующий режим (не ждем getch())

tst = time.time() # Начало работы
wFlag = False # Флаг протоколирования данных в файле, True - пишем файл
ser.readline() # Пропустим парочку значений - обычный мусор
ser.readline()
traw = 13 # Положение таймера при записи файла (
while True:
  '''Обработка возможных событий от клавиатуры'''
  ch = stdscr.getch() # Получаем код нажатой клавиши
  if ch == ord('q'): # Завершение работы
    break
  elif ch == ord('t'): # Коррекция смещения (тары)
    offs = codes60[0] # Корректируем по усредненному за последние 60 сек значению
  elif ch == ord('s'): # Включить/выключить запись в файл
    wFlag = not wFlag
    if wFlag: # Начинаем запись лога
      f = open('log.txt', 'w')
      tstf = tim[0]
      line = '\tВес\t\t\t\tПроизводная\t\t\tКод АЦП\n'
      f.write(line)
      line = 't,сек\t1 сек\t10 сек\t30 сек\t1 мин\t10 сек\t30 сек\t1 мин\t'
      line += '1 сек\t10 сек\t30 сек\t1 мин\n'
      f.write(line)
    else: # В противном случае закроем файл
      f.close()

  '''Работаем с данными'''
  now = time.time() - tst # Текущее относительное время
  try: # Пытаемся получить данные с последовательного порта (от АЦП) 
    code = float(ser.readline().decode())
  except: # Нечисловые данные пропустим
    continue

  codes1 = np.roll(codes1, 1) # "Прокручиваем" все массивы вправо на 1 позицию
  codes10 = np.roll(codes10, 1)
  codes30 = np.roll(codes30, 1)
  codes60 = np.roll(codes60, 1)
  tim = np.roll(tim, 1); tim[0] = now
  codes1[0] = code # Новое значение принятого кода помещаем в начало массива
  '''Массивы небольшие, поэтому рекурентные формулы для сердних не используем,
  а вычисляем средние тупо по всему массиву'''
  codes10[0] = np.mean(codes1[:10])
  codes30[0] = np.mean(codes1[:30])
  codes60[0] = np.mean(codes1)
  mass1 = coef*(codes1[0] - offs) # Считаем соответствующие массы (веса)
  mass10 = coef*(codes10[0] - offs)
  mass30 = coef*(codes30[0] - offs)
  mass60 = coef*(codes60[0] - offs)
  '''Производные считаем при помощи линейной регресии (функция polyfit в 
  numpy) и сразу нормируем результат в g/час.'''
  d10 = np.polyfit(tim[:10], codes10[:10], 1)[0]*cgh
  d30 = np.polyfit(tim[:30], codes30[:30], 1)[0]*cgh
  d60 = np.polyfit(tim, codes60, 1)[0]*cgh

  '''Выводим информацию в файл и на консоль'''
  stdscr.erase()
  if wFlag:
    ltim = '% .1f'%(tim[0] - tstf);
    stdscr.addstr(traw, 20, ltim)
    linem = '%.3f\t%.3f\t%.3f\t%.3f'%(mass1, mass10, mass30, mass60)
    lined = '%.1f\t%.1f\t%.1f'%(d10, d30, d60)
    linec = '%d\t%d\t%d\t%d'%(round(codes1[0]), round(codes10[0]),
                              round(codes30[0]), round(codes60[0]))
    line = ltim + '\t' + linem + '\t' + lined + '\t' + linec
    f.write(line + '\n'); f.flush()

  stdscr.addstr(1, 1, '%.1f'%(tim[0]))
  stdscr.addstr(3, 25, '---------------Окно----------------')
  raw = 4; col = 25; dc = 12
  stdscr.addstr(raw, col, '1 сек'); col += dc
  stdscr.addstr(raw, col, '10 сек'); col += dc
  stdscr.addstr(raw, col, '30 сек'); col += dc
  stdscr.addstr(raw, col, '1 мин')
  raw += 2; col = 2
  stdscr.addstr(raw, col, 'Вес, г'); col += 22
  stdscr.addstr(raw, col, '% .3f'%(mass1)); col += dc
  stdscr.addstr(raw, col, '% .3f'%(mass10)); col += dc
  stdscr.addstr(raw, col, '% .3f'%(mass30)); col += dc
  stdscr.addstr(raw, col, '% .3f'%(mass60))
  raw += 1; col = 2
  stdscr.addstr(raw, col, 'Производная, г/час'); col += 34
  stdscr.addstr(raw, col, '%.1f'%(d10)); col += dc
  stdscr.addstr(raw, col, '%.1f'%(d30)); col += dc
  stdscr.addstr(raw, col, '%.1f'%(d60))
  raw += 1; col = 2
  stdscr.addstr(raw, col, 'Код АЦП'); col += 22
  stdscr.addstr(raw, col, '%d'%(round(codes1[0]))); col += dc
  stdscr.addstr(raw, col, '%d'%(round(codes10[0]))); col += dc
  stdscr.addstr(raw, col, '%d'%(round(codes30[0]))); col += dc
  stdscr.addstr(raw, col, '%d'%(round(codes60[0])))

  raw += 2; col = 2; traw = raw
  stdscr.addstr(raw, col, 'Запись в файл [ ]')
  if wFlag:
    stdscr.addstr(raw, col + 15, 'x')

  raw = 20
  stdscr.addstr(raw, 1, 't - тара (коррекция смещения)'); raw += 1
  stdscr.addstr(raw, 1, 's - вкл/выкл запись данных в файл'); raw += 1
  stdscr.addstr(raw, 1, 'q - выход')
  stdscr.refresh()

# Убираем за собой...
try: f.close()
except: pass
stdscr.keypad(False)
curses.nocbreak()
curses.echo()
curses.endwin()

Скрипт подробно прокомментирован, если кому-нибудь будет интересны детали реализации. Здесь только несколько общих комментариев.

Данные с последовательного порта периодически считываются и помещаются в кольцевой массив из 60 элементов. Затем, по этим данным, вычисляются скользящие средние веса (для окон 10, 30 и 60 сек) и их производные (это наша "скорость отбора"). Производные вычисляются при помощи линейной регрессии по соответствующему количеству отсчетов (функция plyfit() библиотеки numpy). Предусмотрена запись в файл всех данных: время, средние веса и производные веса по времени, рассчитанные в разных окнах усреднения и исходные коды, полученные от ардуинки. Запись производится в обычном текстовом формате. Таблицы потом можно непосредственно загрузить в Libre Calc или Excel для визуализации в виде графиков или дальнейшего анализа. Интерфейс с пользователем осуществляется при помощи библиотеки curses. Вид окна работающего приложения показан на следующем рисунке.

Если кто-нибудь захочет повозиться со своими весами, то скрипт должен работать безо всяких изменений на любом компьютере под Linux. На Ubuntu и Raspbian работал. Если пытаться запускать под Windows, то, возможно, потребуются какие-то танцы с curses. Но точно не знаю. Не пробовал.

3. Шумы ненагруженных весов

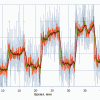
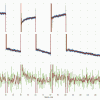
Рассмотрим характер сигналов с ненагруженных весов. Сначала на временном интервале 100 сек. Эти сигналы приведены на следующем рисунке.

Синяя кривая на верхней диаграмме - это, по сути, заводской режим работы - 1 отсчет в секунду безо всякой дополнительной фильтрации (усреднения). Эта диаграмма была записана еще до переключения HX711 в 80-герцовый режим. По характеру сигнала и стандартному отклонению 0.4657, мы видим, что весы вполне вписываются в декларируемую изготовителем точность 1 г. Но нам нужна точность повыше. Поэтому остальные диаграммы получены уже в режиме работы АЦП 80 Гц с применением низкочастотной фильтрацией (усреднения) с периодами (окнами) усреднения от 1 сек и выше. Эти сигналы показаны на этой же диаграмме и, в растянутом масштабе, на нижней диаграмме. Соответствующие стандартные отклонения приведены в легенде справа. Из этих данных легко видеть, что на коротких временах, уровень шума 10-кг весов вполне реально сделать существенно меньше 0.1 г.

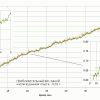
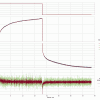
К сожалению, на более длительных интервалах (существенно больших, чем окно усреднения) низкочастотный шум (дрейф) "возвращает" заявленную производителем точность весов 1 г. Это хорошо видно на следующем рисунке, где представлена длительная (более 40 часов) запись сигнала с ненагруженных весов, оставленных на выходные в изолированном, закрытом помещении.

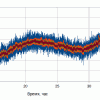
Таким образом, при длительных измерениях веса 10 килограммовыми весами, необходимо ориентироваться на погрешность не менее, чем заявлена производителем. Т.е. - 1 грамм.

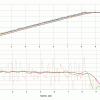
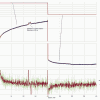
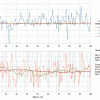
Тем не менее, данные весы предназначены для измерения скорости отбора. Т.е. производной весы по времени. Поэтому интересно было посмотреть шум именно производной, а не самого веса. На следующем рисунке на верхней диаграмме представлена запись производной сигнала ненагруженных весов в течение 10 мин. Для сравнения, на нижней диаграмме приведена соответствующая запись самого веса.

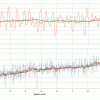
На верхней легенде справа приведены стандартные отклонения производной веса по времени. Эти цифры дают возможность оценить точность, которую можно достичь при различных окнах усреднения. Видно, что при использовании окна 10 сек, мы можем рассчитывать на погрешность измерения скорости отбора никак не менее, чем десяток-другой грамм/час. При отборе голов эта погрешность сопоставима с самой величиной. Для окон 30 сек и 1 мин ситуация лучше - несколько грамм/час и порядка одного грамма/час соответственно. Тем не менее, необходимо учесть, что информацию о нештатном поведении узла отбора мы получим с опозданием на одну-две минуты. Т.е. такие датчики можно использовать лишь для некритических аварийных ситуаций. Ну, например, засорение жиклера клапана отбора...

В следующем топике я расскажу о чувствительности моих 10-килограммовых весов при статических и линейно нарастающих нагрузках.

4. Чувствительность и задержки

Итак, с шумами ненагруженных весов мы разобрались. Общий вывод (насчет шумов) таков: природу можно обмануть, но не надолго :) На временах сопоставимых с размерами окна усреднения. На б'ольших периодах измерения (а нас интересуют именно такие процессы) природа возьмет свое: уровень низкочастотного шума (дрейфа) 10-кг весов будет на уровне своего положенного 1 грамма. 

Теперь самое время разобраться с чувствительностью. Самый простой тест - маленькие разновески на пустых весах или с дополнительными гирями. Я ограничился первым вариантом. На следующем рисунке представлена запись сигнала с весов, на которые я периодически ставил и снимал маленькие разновески. Два раза 100 мг и два раза 200 мг.

Из диаграммы видно, что на коротких промежутках времени вес (0.1 г), на порядок меньший, чем заявленная производителем точность (1 г) вполне надежно регистрируется. К сожалению, из-за низкочастотного дрейфа особого смысла в таких измерениях нет - проще взять другие весы. Поэтому идем дальше.

Следующий шаг важен для рассматриваемой задачи. Необходимо было посмотреть как весы реагируют на медленно линейно растущую нагрузку. Это даст нам какую-то реальную оценку нижнего предела измерения скорости отбора. Для проведения этого опыта, я подвесил на штативе обычную медицинскую капельницу с водой и отрегулировал ее так, чтобы капанье происходило со скоростью примерно одна капля в 25-30 секунд. Капельки капали в небольшую колбу, поставленную на платформу весов. К сожалению, работа таких разовых капельниц не очень стабильна, но кое-какие практические оценки нижнего предела измерения скорости отбора, все-таки, получить можно. Запись сигнала с весов в процессе этого эксперимента показана на следующем рисунке.

Из диаграммы видно, что при использовании окна усреднения 30 сек и 1 мин можно уверенно регистрировать скорости отбора на уровне 1-2 г/час. Это хороший результат. Для большинства наших задач такой точночти вполне достаточно. Интересно отметить ступенчатый характер нарастания веса, причем, высота ступенек приблизительно равна массе одной капельки (0.02 г, капельки маленькие, с кончика иглы от шприца). Таким образом, по части регистрации медленно и линейно нарастающего веса никаких претензий к этим весам нет.

Ну и в завершение экспериментов с капельницей, я установил скорость нарастания веса около 40 г/час (для спирта это будет соответствовать "типовой" скорости отбора голов 50 мл/час) и, через некоторое время, быстро перекрыл капельницу. Ну, как бы моделируя засорение отверстия жиклера клапана отбора :) Соответствующие диаграммы представлены на следующем рисунке.

На верхней диаграмме зависимость веса на платформе от времени, на нижней - производной веса по времени времени. Т.е. - скорости отбора. Ровно на 8-й минуте я перекрыл капельницу. Из нижней диаграммы хорошо видно, что сигнал производной с 10 секундным окном усреднения сильно зашумлен. Фактически уровень шума сопоставим с уровнем самого сигнала. Т.е. окно усреднения 10 сек явно не подходит для задачи непосредственного контроля скорости отбора. В то же время, кривые производных с окнами усреднения 30 и 60 сек вполне четко регистрируют ступеньку, сигнализирующую о прекращении поступления жидкости. К сожалению - с задержками порядка 30 и 60 секунд (на уровне 50% сигнала) соответственно. Поскольку эти задержки принципиально неустранимы, то становится ясным, что для критических аварий такой метод измерения скорости отбора явно не годится. Одно дело, когда жиклер клапана отбора засорился, а совсем другое - когда трубка насоса рвется...

Остается проверить еще одну группу параметров весов - динамику релаксации сенсоров при импульсном нагружении и разгрузке. Нагружение нам не очень важно, а вот разгрузка как раз очень интересна. Дело в том, что можно попытаться снять противоречие между требованием высокой точности и большим предельным весом весов за счет организации периодического слива накопленного в приемной емкости продукта. Это дало бы возможность использовать весы с относительно небольшим предельным весом (0.5-1 кг и менее), но с высокой точностью (0.1-0.01 г), что позволило бы создать действительно малоинерционный датчик скорости отбора. Об этих опытах я расскажу в следующем топике.

на 40 часовом графике скорее всего температурный дрейф или тензодатчика или АЦП

скорее всего температурный дрейф или тензодатчика или АЦПdee, 04 Нояб. 19, 14:22

Все может быть... Конечно, я специально температуру не контролировал. Хотя ее колебания в закрытой комнате без сквозняков не должны быть велики. Тем более, что причин для дрейфа нуля весов хватает и без температурный колебаний. Питание, например. Малинка питается далеко не от самого совершенного импульсного источника питания. А от нее через USB запитывается ардуинка и затем уже АЦП.

Но, на самом деле, причина дрейфа не так уж и важна. Важно то, что суммарный дрейф нуля весов почти за двое суток все-таки не выходит за рамки декларированной точности (1 г). Это неплохой результат. Суть опыта как раз и была в том, чтобы понять что будет с весами при длительной (многосуточной) непрерывной работе. Все-таки, ректификация - дело долгое.

Интересно отметить ступенчатый характер нарастания веса, причем, высота ступенек приблизительно равна массе одной капельки (0.02 г, капельки маленькие, с кончика иглы от шприца).OldBean, 04 Нояб. 19, 13:52

Не знаю кому это нужно и зачем.. Но если вдруг стоит проблема счета одиночных капелек - то если взять в качестве датчика телефонный капсюль типа ТОН-2 1600 Ом, и использовать его металлическую мембрану в качестве микрофона - то он очень чувствителен, если правильно подобрать схему усилителя..

Во всяком случае - капельки спирта от инсулиновой иголки - без проблем улавливались с высоты 5 см.. 

ЗЫ..  Лично я как ни корячился, присунуть это чудо техники - в практическое применение у меня так и не получилось, по причине полной бесполезности капельного учета.. (большое ИМХО)..

Не знаю кому это нужно и зачем..Zapal, 05 Нояб. 19, 02:22

Не-не... Тут никакого прикладного смысла, связанного с капельками, не закладывается. Просто иллюстрация чувствительности кухонных 10-кг весов: при декларируемой точности 1 г они все-таки могут стабильно регистрировать изменения веса почти на два порядка меньше - на уровне не хуже 0.02 г.

Не знаю, наверное у метрологов есть специальный термин для этого. Но я по-простому, по-физически: это как оценка своеобразной "силы трения покоя". Ну вот когда сахар пытаешься точно отмерить. Под конец сыпешь уже почти по песчинке, а показания весов стоят и никак "не страгиваются". А потом - бац! И все-таки пересыпал... :)

Поскольку эти задержки принципиально неустранимы, то становится ясным, что для критических аварий такой метод измерения скорости отбора явно не годится. Одно дело, когда жиклер клапана отбора засорился, а совсем другое - когда трубка насоса рвется...OldBean, 04 Нояб. 19, 13:52

да брось...1 минута — это вообще ниочем.
Даже если у тебя колонна 2кВт, и даже если предположить что оторвался штуцер дефлегматора, то за минуту мы потеряем 4500х2/60=150мл флегмы.
А за 30 секунд — 75мл

Сомневаюсь я, что датчик разлития воды на полу способен среагировать быстрее)))

1 минута — это вообще ниочемигорь223, 05 Нояб. 19, 08:17

Все относительно - тут уж каждый сам решает... Дело не в потерях, а скоре - в окружении и в том куда это все будет попадать. Для кого-то забрызгать лабораторный журнал - великое горе, а кто-то, надев сапоги, вычерпает ведро-другое с бетонированного поля и бровью не поведет...

В приведенном примере (про оторванный штуцер), правильней было бы ориентировать не на пролитое количество, а на время, которое нужно чтобы "заглушить" куб (или - на принятие других мер остановки процесса). Если оно больше 1 мин, то инерция датчика в 30-60 сек не скажется существенно на быстродействии всей защиты. А если много меньше, то лимитировать скрость защиты будет уже сам датчик. Это не значит, что им нельзя пользоваться. Это значит, что применено плохое (точнее - неадекватное) инженерное решение. ИМХО.

5. Релаксация и гистерезис

В завершение темы, нам осталось посмотреть как ведут себя нагруженные весы. К сожалению, точных гирь (на 5-10 кг) у меня под рукой не оказалось. Но мне точная калибровка в общем-то и не была нужна. Поэтому я воспользовался одним из свинцовых кирпичей, найденных в закромах. Он весит чуть более 5.5 кг. Т.е. чуть больше половины максимальной нагрузки. Для эксперимента с нагруженными весами - в самый раз.

Схема эксперимента простейшая: включаем запись данных в файл, максимально "нежно" кладем свинцовый кирпич на весы. Запись в файл непрерывно производится. Через некоторое время также аккуратно снимаем кирпич, продолжая запись. Результат показан на рисунке ниже.

Рис.10

На верхней диаграмме - обзорный график зависимости веса от времени. Там ничего интересного нет - прямоугольный импульс. На следующей диаграмме - сама "полочка" этого импульса. Масштаб по весу сильно растянут. На диаграмме хорошо виден классический профиль упругой ползучести (упругого последействия). Как и положено, скорость последействия постепенно уменьшается, но окончания релаксации я ждать не стал - на двухсотой минуте снял груз. На третьей диаграмме представлен профиль разгрузки. Тоже с сильно растянутым масштабом по весу. Хорошо прослеживается отрицательное упругое последействие. Ну а на самой нижней диаграмме - графики производной веса по времени (это как бы "скорость отбора" :)

Их диаграмм видно, что релаксация очень длительная. Часы! К сожалению, я не специалист по сопромату. Поэтому мне трудно сказать что-то определенное о причинах такой длительной релаксации тензодатчиков. Насколько я знаю, железяки, релаксируют гораздо быстрее. Чуть ли не секунды. А тут - часы... Но экспериментальный факт - есть факт. Увы, но данный опыт немного отрезвляет голову по вопросам точности весов. Получается, что именно из-за такой длительной упругой ползучести мы не можем говорить не только о 0.1-граммовой точности весов, но и даже о декларированной 1-граммовой. Реальная точность данных 10 кг кухонных весов в середине диапазона будет на уровне 10 г (а может быть даже и хуже, поскольку конца релаксации я так и не дождался). Интересно, при этом, что локальная реакция весов на небольшие разновески (см. ступеньку на второй диаграмме) вполне адекватная. Ступенька в 500 мг на разновеску 500 мг. Но упругая ползучесть все портит. Относительная ошибка, конечно же, остается небольшой. Она порядка одной-двух десятых долей процента. Для обычного взвешивания - этого более чем достаточно. Но для независимых дифференциальных измерений такой точности уже явно недостаточно.

Смотрим далее. Из третьей диаграммы, где отрицательное упругое последействие, легко видеть, что после отрицательной релаксации (после разгрузки весов), "ноль" почти вернулся к первоначальному значению. Невязка - не более полутора граммов. Вероятно, эта невязка вызвана двумя причинами: гистерезисом и долговременным дрейфом нуля весов, который, как мы уже видели в предыдущих опытах, составляет величину порядка грамма. Для оценки гистерезиса рассмотрим результат следующего опыта. В этом опыте я несколько раз, не дожидаясь окончания релаксации, ставил и снимал груз (этот же самый свинцовый кирпич) с весов.

Рис.11

Из этих графиков мы можно сделать грубую оценку гистерезиса - примерно на уровне полграмма. Оценка, конечно, очень грубая, но точная здесь в общем-то и не нужна. Видно, что смещение от гистерезиса примерно такое же, как и от дрейфа. Сопоставимые эффекты. А в целом - на уровне декларируемой точности весов (1 г).

Из приведенных в этом топике диаграмм производной веса следует еще один вывод. Из-за длительных упругих последействия тензодатчиков, возникают систематические ошибки при измерении производной (т.е. скорости отбора). Эта ошибка положительная при нагружении и отрицательная при разгрузки весов. В начале релаксации и в течении десятка минут она составляет величину порядка 10 г час и -5 г/час соответственно. В целом это не очень много. На уровне погрешностей от шума. Тем более, что длительность релаксации при разгрузке заметно меньше, чем при нагрузке. Таким образом, идея организации измерений скорости отбора с периодическим сбросом продукта из взвешиваемой приемной емкости, может оказаться вполне состоятельной.

6. Выводы

Итак, резюмируя наше краткое "полу-количественное" знакомство с 10-кг кухонными USB-весами, можно сформулировать следующие выводы.

1. Измерение веса
   1.1. В начале шкалы, за счет повышения частоты работы АЦП до 80 Гц и использования низкочастотной фильтрации (скользящего усреднения) можно добиться точности взвешивания не хуже 0.1 г. Но особого практического смысла в этом нет, т.к. для небольших масс можно просто взять другие, более точные весы с меньшим предельным весом.
   1.2. В середине диапазона (5 кг) в качестве оценки точности весов можно взять 7-10 г. Основная причина увеличения погрешности к середине диапазона (и далее) - длительный (несколько часов, возможно больше) период упругого последействия, заведомо превышающий разумные времена взвешивания. При этом возникает много неопределенностей, связанных с моментом фиксации веса эталона при калибровке, как распределится упругая ползучесть в случае дробного набора веса и т.д. Поэтому для оценки точности мы и должны брать полную величину последействия. Точность в конце диапазона я не оценивал, но вряд ли она будет лучше. А скорее - еще хуже.

2. Измерение скорости отбора
   2.1. Точность измерения скорости отбора (производной веса по времени) в начале весовой шкалы определяется в основном длительностью окна усреднения (несколько г/час и хуже при окнах усреднения до 60 сек). Дополнительную погрешность (до 1 г/час) вносит и дрейф нуля весов.
   2.2. По мере нарастания веса, становится существенным вклад упругой ползучести. Для линейно нарастающей нагрузки опытов не проводилось, но для импульсной (5.5 кг) - это величина порядка десятка г/час.

3. Инерция измерений
   В проведенных опытах использовалась низкочастотная фильтрация. Фильтрация применялась как к весу, так и к производной веса по времени. В связи с этим, для измеряемых величин характерна некоторая задержка. Величина задержки пропорциональна размеру окна усреднения. При измерении производной, окна короче 30 сек дают сильно зашумленные значения. Поэтому, для использования таких весов в качестве датчика скорости отбора, необходимо ориентироваться на окно 30 сек, а лучше - 60 сек. Поэтому реальные задержки, с которыми мы будем иметь дело будут порядка минуты и более. Это - плата за фильтрацию. Кстати, ручная регулировка скорости отбора по показаниям такого инерционного датчика потребует железных нервов от оператора :)

---

PS
Решил провести еще парочку записей - оценить длительность релаксации в середине и конце шкалы. Оставил на ночь. Вечером оставлю два кирпича (весь диапазон) на выходные. Тогда и сделаем окончательные выводы по поводу точности этих весов.

7. Дополнение

Сделал "контрольный" опыт с весами для оценки их точности в конце диапазона. В пятницу после обеда, предварительно включив запись веса в файл, аккуратно положил на весы два свинцовых кирпича (чуть более 11 кг). Вчера по дороге заскочил к весам и снял эти кирпичи. В результате получил профиль веса с высоким разрешением. Результат представлен на картинке ниже.

Первое, что видно из этой картинки - это то, что вес практически вернулся к нулю. Это действительно обратимый эффект. Т.е. мы имеем дело упругим последействием. Или, другими словами, - с упругой ползучестью. Остальные дрейфы (термо- и электро-) относительно невелики.
Второе - ползучесть о-о-очень медленная. Порядка суток. Но, для измерения скорости отбора - это, скорее, положительный фактор. За исключением моментов времени в час-другой после импульсного нагружения (или разгрузки), вклад скорости релаксации в производную становится пренебрежимо малым по сравнению с шумом производной.
Третье. Эффект упругого последействия - сильный эффект (по сравнению с дрейфами и шумами). В конце диапазона весов измеренное положительное последействие не менее 13 г, а отрицательное (после разгрузки) - 8 г. Т.е., похоже, что именно упругое последействие и определяет реальную абсолютную ошибку 10 кг весов - не лучше 10 г. Относительная ошибка - на уровне 0.1%. Для абсолютных измерений - неплохая точность, для дифференциальных - плохая.

Окончательные выводы

1. 10-кг кухонные весы с тезодатчиками на ножках - неплохие весы для абсолютных измерений: отвешивать сахар, дрожжи, измерять общее количество отобранного спирта в приемной емкости и т.п. Работают стабильно, малочувствительны к обычным "бытовым" шумам.
2. При проведении независимых дифференциальных измерений следует иметь в виду большую абсолютную погрешность на уровне 10 г в середине и конце диапазона весов и длительные времена релаксации. Эти факторы следует учитывать при разработке методики измерений.
3. Данные весы вполне могут быть использованы для измерения скорости отбора с точностью до нескольких грамм в час и временем запаздывания порядка минуты-двух.
4. Скорость релаксации в течение первого часа после разгрузки составляет отрицательную величину порядка 10-20 г/час. Этот фактор тоже следует учитывать, если планировать систему с периодическим сбросом накопленного продукта из приемной емкости (чтобы система не воспринимала резкое уменьшение скорости отбора как неисправность узла отбора :)

---

Ну вот теперь, наверное, все. 10-кг весы о 4-тензодатчиках на ножках мы "почувствовали". Можно закрывать тему.

Все-таки специализация - великое дело. Единственные "универсальные весы" для контроля отбора - не самая лучшая идея. Правильное решение - использовать двое весов. Большие и маленькие. Большие весы (как, например, "изученные" здесь, 10-килограммовые) - для контроля общего количества отобранного продукта, а маленькие весы (грамм на 100-200) - для контроля скорости отбора. Это так. Я вчера проверил. Пример малоинерционного датчика скорости отбора на 100-граммовом тензодатчике можно посмотреть здесь.

Не сдержался... Не хотелось что то писать на данном форуме из за первоначального "приема", но все же.

Вот только на практике все и с 10 кг. тензодатчиком работает на ура, и с датчиком на 40 кг., но с чуть большей погрешностью (пляской показаний) совершенно на практике не критичной, ссылку на видео к сожалению вставить форум не дает, не достоин пока )))
У меня сейчас замер веса производится 5 - 6 раз в секунду (вывод на дисплей и связь по WiFi, не имеют постоянного временного интервала, поэтому плавающая временная составляющая присутствует), цифровая фильтрация тоже присутствует в коде. Обрабатываются данные за минутный интервал со сдвигом данных в массиве для расчета скорости отбора. Все кто начал пользоваться данным вариантом, просто забыли про пробирки и секундомеры.
Оно конечно радует, что у Вас есть столько свободного времени на лабораторные эксперименты. Но проще и быстрее было в живую все собрать и попробовать, а не "парить" народу мозг, что все это полная хрень (извиняюсь за выражение). Я конечно понимаю, что есть определенные факторы, вносящие некий дисбаланс в наши измерения. Точнее, самых критичных, всего три: 1) усталость металла, приводящая к постоянному сползанию показания веса, но 10 гр., и даже 100 гр. за сутки, нам как то "по барабану"; 2) разброс характеристик сопротивлений измерительного моста, в том числе температурных; 3) погрешность примененного АЦП и наводки на провода к тензодатчикам. Но мы не атомы в ядерной промышленности измеряем. Для наших нужд, это на данный момент лучший вариант (просто/дешево/функционально) одновременного измерения и объема продукта, и скорости его отбора. При определенном шевелении мозгом, к данному функционалу можно привязать алгоритмы любой автоматики, так сказать к одному нажатию кнопки "Старт".

p.s. В общем то я все это пишу не для того чтобы сказать кто хороший а кто нет, просто обидно, когда неправильные (ошибочные) умозаключения уважаемого человека на данном форуме, отпугивает народ от упрощения своей "винокуренной" жизни. Мне совершенно без разницы, соберет народ мои весы, весы Андрея (кстати весьма не плохой проект), или сделает что то свое. Но определенными высказываниями, тем более с приведением именно Ваших исследований, предполагаю с "безобразным" одноразовым монтажом самой схемы, отпугивает народ от каких бы то не было разработок именно в данном направлении.

Для наших нужд, это на данный момент лучший вариант (просто/дешево/функционально) одновременного измерения и объема продукта, и скорости его отбора.serjrv, 13 Дек. 19, 00:07

Если прикладывание весов к больному месту облегчает течение геморроя, то кто же мешает прикладывать? Весы в руки, если помогает. Но зачем же возмущаться, если кто-то обоснованно не хочет прикладывать? Вы скажите ЧТО конкретно из того, что я привел в этой ветке, Вы считаете ошибочным, а я постараюсь объяснить свою точку зрения на данный вопрос. Или же согласиться с Вашим возражением, если не прав.

У меня сейчас замер веса производится 5 - 6 раз в секунду (вывод на дисплей и связь по WiFi, не имеют постоянного временного интервала, поэтому плавающая временная составляющая присутствует), цифровая фильтрация тоже присутствует в коде. Обрабатываются данные за минутный интервал со сдвигом данных в массиве для расчета скорости отбора.serjrv, 13 Дек. 19, 00:07

А тогда можно программу выложить?

Если прикладывание весов к больному месту облегчает течение геморроя, то кто же мешает прикладывать? Весы в руки, если помогает. Но зачем же возмущаться, если кто-то обоснованно не хочет прикладывать?OldBean, 13 Дек. 19, 04:18

Почему то совсем не удивлен, столь грубым ответом.
Для начала, поместите в экран все провода идущие к тензодатчикам. Еще обратите внимание, что тензодатчики в выбранных Вами весах стоят не правильно, опорные ноги весов смонтированы прям на измерительные мосты тензодатчиков. Усреднение по 80 отсчетам АЦП применять просто глупо, т.к. есть более продвинутые алгоритмы цифровой фильтрации сигнала.
Устраните хотя бы приведенные ошибки, а уже потом производите какой то анализ своих изысканий. Хотя и это не факт что поможет, т.к. противоречите сами себе. Приходите к выводу что есть ползучесть веса, хотя можно было и без экспериментов сопромат вспомнить, и тут же предлагаете замерять скорость отбора с периодическим опорожнением емкости, т.е. сознательно повышая погрешность.

А тогда можно программу выложить?surami56, 13 Дек. 19, 08:25

В теме про датчик скорости отбора на Arduino, я писал как найти информацию по упомянутым весам. Дублировать информацию на разных форумах смысла не вижу. Приводилась вся информация для сборки, правда сам код программы в открытый доступ пока не выкладывал, только уже скомпилированная прошивка, т.к. еще не все свои задумки реализовал. Хотя всем кто просил исходники программы, все предоставлял.

Почему то совсем не удивлен, столь грубым ответом.serjrv, 13 Дек. 19, 10:22

А что Вы хотели получить на откровенный троллинг? К сожалению, второй топик недалеко ушел от первого. Мне есть что ответить, но, увы, расхотелось тратить время на общение с Вами.

Подниму тему.
К ардуине прикрутил весы 1 кг. Измеряют само собой общий вес и скорость отбора. Т.е. можно задать колличество голов и их скорость. Затем начальную скорость тела не прыгая с секундомером и пробиркой. Если кому интересно.
Либо вовремя сливать. Либо весы посерьезней.
Жёлтое скорость отбора г/час, бирюза общий вес. Неравномерность из за малого периода отсчёта. 12 секунд соизмеримо с колл капель. Не суть.
В планах завести на автоматику отбора. У меня серва. Для клапана проще. Включил. Отсчитал вес. Выключил. Отсчитал время. Включил. Прямое вычисление отбора.
Косяки весов помню.

Добавлено через 10дн. 7мин.:

Всё на соплях. Тем не менее. Проверка адекватной работы на струе голов. В смысле чувствительность. Дальше будет проще.

Косяки весов помню.Виктрыч, 15 Марта 23, 09:27

Косяки весов на HX711 можно победить, если вместо hx711 использовать микросхему от Analog Device AD7799. Относительно высокая точность и отсутствие плавания у нее , по сравнению с HX711. При подключении 2-х тензодатчиков по 50 кг по мостовой схеме точность 10 грамм. Использую библиотеку AD779x.h и пример программы, который появляется в меню файл-примеры в ардуино, после установки библиотеки. При подключении hx-711 к этим-же датчикам у меня точность составила 30 грамм, измерял точность у обеих АЦП в течение 10 минут. Заказывал AD7799 на али за 250 руб. Брать нужно вместе с переходником для микросхемы ssop16 c расстоянием между выводами переходника 0,65 мм. Также нужно брать "паяльная паста с припоем", т.к. выводы слишком мелкие и близкие. Конденсаторы брал SMD с испорченной матплаты, измеряя их емкость тестером. При прогреве тензодатчика феном , данные сильно изменяются. Возможно нужно ставить на тезодатчик на термоскотч термодатчик цифровой ds18b20. При даже кратковременном прикосновении к тензодатчику пальцем показания также сильно изменяются из-за прогрева датчика от тепла тела. Если прикасаться через несколько слоев сложенной бумаги, датчик не прогревается и показания не меняются. Те, кто будут тестировать тензодатчики, нажимая на них пальцем, должны помнить, что через несколько секунд, после прикосновения пальца к тензодатчику, тепло достигнет чувствительного элемента датчика по его металлическому корпусу и значения поплывут наверх или вниз на десятки грамм, в зависимости от схемы подключения, типа датчика, длительности прикосновения. Нажимайте на датчики какими либо предметами, а не рукой напрямую. L индуктивность возможно можно и не ставить. Возможно можно подключить и без источника опорного напряжения TL431, а напрямую от ардуино 5в с фильтром из 2-х конденсаторов (что на схеме). Я сначала подключил без него и показания были вполне нормальные. Нужно пробовать... Источник питания использовал от Hi-link. Надеюсь, кому-то схема и инструкция помогут. Интернет наводнен попытками сделать из hx711 конфетку у ардуинщиков.

Vache, Вы точно в схемотехнике разбираетесь, или просто эксперименты из доступных схем и модулей Алишных проводите?
HX711 прекрасно работает с НОРМАЛЬНЫМИ тензодатчиками, вот только схема включения якобы прецизионного напряжения на сам тензодатчик выполнена "бардачно", и любой вменяемый схемотехник это видит сразу. Проще говоря, опорка на датчик в стандартной схеме с Али, реализована через попу, как в принципе и в даташите, хотя и соответствует заявленным характеристикам. Реализуйте опорку вменяемо, и все встанет на свои места. А так, HX711 с ее рекомендуемой схемой включения, разрабатывалась совершенно для другой точности измерений, и она заявлена в доках. По поводу термостабильности, думаю вам точно двоечку можно впаять, а если еще и работа с этим связана, я бы вас выгнал к чертям... Мостовая схема термостабильна по определению, если конечно мы там проводники с разным ТКС не используем. А вот не учитывать что половинки моста расположены с разных сторон единичного тензомоста (а в вашем случае еще и разнесенных), и нагревать не все в комплексе, полный бред.

Мои претензии к весам на 711 на сегодняшний день такие:
1.Из 8килограммовых килограммовые весы сползли до 4 кг. Ну дык они не виноваты, что на них столько валили и загнули. Можно разогнуть. Или на 10 прицепить. Но для трехлитровки килограммовые в самый раз в моём аатоматике. Задаю 2400 по умолчанию. Это 3 л спирта. Тара 900 сброшена. Накапало, пищит. Не подходишь, финишь. Этот пункт решаем. Ну пусть сползут за 5 часов на 5 грамм.
Можно по калькулятору Руди задать гудок допустим на 10% в струе зная вес или объём куба и его спиртуозность. Которые опять же можно вычислить по его весу и точке кипения. Есть куда расти. Ещё бы исходники калькулятора где-нить найти. Так что это даже не претензия.
2. Задуманый расчёт скорости струи по весу делает приличную моментную ошибку. Шумят. На отборе голов допустим 50г/час могут показать 25,а через минуту 75. А если прилетит редкая помеха, зашкалит. Можно отфильтровать для дисплея, но для автоматики не годится. Для моей. Пока этот пункт отложен.

Добавлено через 40мин.:

Вот дрейф моих весов по включению. В перерасчёте на отбор пока максимальная ошибка 9г/час.Вполне себе. Понаблюдаю.

Добавлено через 9мин.:

ПС. 1,2 и 4 колонки как понятно температуры рядом валяющихся датчиков. Заслуживающей внимания связи с весами не увидел.