Теория фазового состояния водно-спиртовой смеси: температура, давление, концентрация

Чтоб не забыть прикопаюка я нужные формулки...

Перевод массовых долей A в молярные доли X

Скрытый текст

Function XsAs(aAs As Double) As Double
   Ss = 46.07    ' Молярная масса спирта
   Sw = 18.01528  ' Молярная масса воды
   XsAs = aAs * Sw / (Ss - aAs * (Ss - Sw))
End Function

Function XsAw(aAw As Double) As Double
   Ss = 46.07
   Sw = 18.01528
   XsAw = (1 - aAw) * Sw / (Sw + aAw * (Ss - Sw))
End Function

Function XwAw(aAw As Double) As Double
   Ss = 46.07
   Sw = 18.01528
   XwAw = aAw * Ss / (Sw + aAw * (Ss - Sw))
End Function

Function XwAs(aAs As Double) As Double
   Ss = 46.07
   Sw = 18.01528
   XwAs = (1 - aAs) * Ss / (Ss - aAs * (Ss - Sw))
End Function

Эпиграф:
Ученые взяли грант на разработку технологии переработки говна в сливочное масло.
Когда пришло время сдавать отчет написали следующее:
"На хлеб уже мажется, но запах пока не устранили"

Давно не писал в этой ветке, но тему не забросил, а иногда даже гонял в компьютере формулки...
Оказалось, что  задача весьма наукоемкая, а я в термодинамиках не особо силен к сожалению,
но кое до чего докопаться всё же удалось.
Огромное подспорье в этом оказал реверс-инженеринг программы [сообщение #12892126] уважаемого OldBean,
еслиб не она, я бы так и не понял как всеми этими термодинамическими формулами пользоваться,
в книжках и статьях всё написано настолько заумно, что не имея начальной базы,
разобраться практически не реально.
Но наглядный пример использования этих формул помог сделать первый шаг в понимании их практического использования.
В частности стал понятен описанный в Стабникове алгоритм расчета температуры кипения спирто-водяной смеси,
и даже надыбанная 223им шикарнейшая статья [сообщение #12855025]

Докладываю что сделано на текущий момент.

Надыбаны точнейшие американские данные по фазовому равновесию для чистой воды,
найдены аналогичные данные советского происхождения,
проведено сравнение и выяснено, что советские и американские данные имеют  между собой довольно приличное расхождение.
Т.к. американские данные имеют меньшие шумы в интересующем нас диапазоне за основу расчета были взяты они.
Найдены данные для переохлажденной воды, вплоть до -80°С, но качество данных для температур ниже -50° весьма посредственное, годится только для ориентировочных вычислений. К тому же есть статья утверждающая что ниже -45°С вода вообще не может существовать в жидком виде, что ещё больше подрывает доверие к низкотемпературным данным.

По приведенным данным построена точнейшая формула. Точность формулы гораздо выше чем расхождение между таблицами экспериментальных данных из разных источников. Сразу понятно что формула брехливая, т.к. она не проходит через тройную точку воды, положение которой измерено с просто охренительной точностью. Но это не проблема моей апроксимации, а проблема собственно исходных данных, которые имеют достаточно ощутимую систематическую погрешность. Случайная погрешность при апроксимации была сильно уменьшена за счет усреднения по большому количеству точек.

Формула для воды:

Скрытый текст

Function Water_Py(t As Double) As Double
   A = 11.970688648
   B = 4024.583379917
   C = 236.150091206
   X = A - B / (t + C)
   Water_Py = X

       B0 = 0.000004249603366
       B1 = 0.000002156940684
       B2 = -0.000002275100059
       B3 = -4.482232677E-07
       B4 = 1.324494537E-07
       B5 = 3.182491698E-08
       B6 = 1.634867824E-09
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6)
       
   If (X > 2.26) And (X < 3.94) Then
       B0 = 1.889652377
       B1 = -7.467779391
       B2 = 11.466933764
       B3 = -9.390740716
       B4 = 4.588354251
       B5 = -1.386477517
       B6 = 0.25490024
       B7 = -0.026194438
       B8 = 0.001155861
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6 + B7 * X ^ 7 + B8 * X ^
   End If
   
   If (3.94 < X) And (5.27 > X) Then
       B0 = 3229.82465378
       B1 = -5720.029975593
       B2 = 4423.431988826
       B3 = -1950.890510526
       B4 = 536.691640265
       B5 = -94.302671542
       B6 = 10.335237756
       B7 = -0.645932988
       B8 = 0.017625184
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6 + B7 * X ^ 7 + B8 * X ^
   End If
   
   If (4.6 < X) And (5.27 > X) Then
       B0 = 0.0002318977291
       B1 = -0.00005229571705
       Water_Py = Water_Py + (B0 + B1 * X)
   End If
   
   
   If (5.27 < X) Then
       B0 = 7681.790742263
       B1 = -5775.796589055
       B2 = 1628.536919808
       B3 = -204.082566539
       B4 = 9.590707189
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4)
   End If
   
   If X <= -2.5 Then
       B0 = 0.035372644
       B1 = 0.028785789
       B2 = 0.011656783
       B3 = 0.003550841
       B4 = 0.0005410203514
       B5 = 0.00003784249943
       B6 = 0.000000997492604
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6)
       Exit Function
   End If
   
   If X <= 3 Then
       B0 = 0.015974026
       B1 = 0.001970845
       B2 = -0.002650808
       B3 = -0.0001954949472
       B4 = 0.0000385473092
       B5 = 0.000006762516256
       B6 = 5.200317273E-07
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6)
       Exit Function
   End If
       
'        Exit Function
   
   If X > 2.99 Then
       B0 = 96.661584114
       B1 = -197.292239424
       B2 = 175.288633343
       B3 = -88.537438352
       B4 = 27.807528117
       B5 = -5.561745048
       B6 = 0.69188409
       B7 = -0.048953459
       B8 = 0.001508635
       Water_Py = Water_Py + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5 + B6 * X ^ 6 + B7 * X ^ 7 + B8 * X ^
       Exit Function
   End If
Exit Function
   
End Function

Аналогично были найдены и обработаны данные по чистому этиловому спирту.

Формула для спирта:

Скрытый текст

Function Ethanol_Py(t As Double) As Double
   A = 11.911817251
   B = 3617.972455928
   C = 225.272718036
   X = A - B / (t + C)
   
   If X < 0 Then
       B0 = 0.00007547093051 + 0.019569576
       B1 = 0.00004067749164 + 0.007666998
       B2 = 0.000004095208056 + 0.0004004972163
       B3 = 1.276671113E-09
       B4 = -1.051754195E-08
       B5 = -2.385993696E-10
   Else
       B0 = 0.019566762 - 0.00006934724351
       B1 = 0.010931881 + 0.00002598621517
       B2 = -0.00697901 - 0.000001768091921
       B3 = 0.003506054
       B4 = -0.001980306
       B5 = 0.0002945321455
   End If
   Ethanol_Py = X + (B0 + B1 * X + B2 * X ^ 2 + B3 * X ^ 3 + B4 * X ^ 4 + B5 * X ^ 5)
End Function

Как видно формулы не особо удобные для расчетов, а особенно для пихания в микроконтроллер.
На этот счет есть идеи запихнуть обе формулы в кубический сплайн.
Зависимости очень плавные, на таких данных сплайн дает потрясающую точность интерполяции,
при затрате достаточно небольших вычислительных ресурсов.

На графиках приведены графики относительных погрешностей полученных формул.
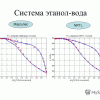
И приведены зависимости давления от температуры для воды и спирта на одном графике, видно что нам следует делать дальше,
сначала по температуре находим "вилку" давлений, между давлением чистой воды и чистого спирта,
затем используя зависимость давления смеси спирта и воды от температуры и спиритуозности находим обратную функцию и получаем искомую спиритуозность для заданного давления.

Формулы конечно муторные, но главное что теперь есть понимание куда двигаться.

Добавлено через 3дн. 8ч. 41мин.:

Добрадся наконец то до смеси Спирт-Вода
Забил взятые из Стабникова экспериментальные данные по активностям воды и спирта в эксел
и построил графики.
Получается что зависимость активностей от давления довольно слабая и закономерности
зависимости коэфициентов активности от давления не просматривается.
Зато видно что уравнение Ван-Лаара дает умеренно хорошую апроксимацию экспериментальных данных.
Уравнение Цубоко-Катаямы (по отзывам более точное) пока запрограммировать не удалось, и нет пока понимания причины почему оно дает не корректные результаты.

Помнится 221ый просил использовать в качестве опоры Калькулятор Руди со старыми таблицами
Ваше желание исполнено! 
Сделал пробный расчет для 101.3 кПа
и сравнил результат с таблицей из Стабникова и с калькулятором Руди.
Как не странно калькулятор Руди шумит меньше чем Стабников.

главное что теперь есть понимание куда двигаться.Kotische, 06 Июля 19, 21:20

У кого есть понимание того, что происходит в этой ветке, стесняюся спросить?
)))

Как что?!
Научно-прикладная НИР.
Пытаемся получить абсолютно точную формулу,
которую можно было бы легко запихнуть в чахлый микроконтроллер.

Ты это... спрашивай, если что не понятно ))))

А, ну тогда внимательно внемлю, продолжаю вяло следить за полетом мысли научного исследователя.
Когда надо будет аплодировать стоя, маякуй...и это: на входе есть показания термометра и барометра, на выходе — нужны обьемные проценты в паре и в кубовом остатке.

Как видишь, постановка задачи проста и неизменна!

Добавлено через 1мин.:

Непонятно пока одно — как это решить с помощью современной микропроцессорной техники

на входе есть показания термометра и барометра, на выходе — нужны обьемные проценты в паре и в кубовом остаткеигорь223, 10 Июля 19, 21:41

Это всё на самом деле такая мелочь...
я уже давным давно все формулы для пересчета из молярных долей в объемные вывел, и даже здесь не однократно выкладывал.
Вот перевести их одних долей в другие - ну вообще не проблема.
Проблема найти давление для ПРОИЗВОЛЬНОЙ спиритуозности!
Вот это пока не решенная до конца задача, с ПРЕДЕЛЬНОЙ точностью.
А если ограничится точностью 1 кПа, то формула уже сейчас дает такую точность относительно калькулятора Руди (посмоттри картинку).
С таблицами Стабникова не бьется сильнее, но они стремные какие то.

Я вот думал ты сейчас скажешь что такие формулы в микроконтроллер хрен запихнешь,
и даже ответ тебе на это заготовил...
но ты как то этот вопрос обошел стороной, видимо сами формулы не смотрел

Добавлено через 1мин.:

Непонятно пока одно — как это решить с помощью современной микропроцессорной техникиигорь223, 10 Июля 19, 21:41

О! заметил таки! )))))))

как это решить с помощью современной микропроцессорной техникиигорь223, 10 Июля 19, 21:41

На самом деле, именно эти формулы не нужно пихать в микроконтроллер.
Я выше упоминал кубический сплайн, это крутейшая штука для интерполяции таблично заданных функций.
Свойства найденных функций таковы, что они очень хорошо приблизятся сплайном, для которого не нужен мощный процессор.
А муторные формулы у меня исключительно для эксела, в котором нифига нет нормальных массивов и структур.
Зато в таком виде их очень удобно в экселе подгонять под нужный график функции.

пихать в микроконтроллерKotische, 10 Июля 19, 21:54

Дык не нужно пихать в микроконтроллер формулы для всего мысленного диапазона давлений/температур/концентраций. Микроконтроллер вещь специализированная (узкоспециализированная). Загнать в него нехитрый сплайн или полином для нужного узкого диапазона и voi la !

Проблема найти давление для ПРОИЗВОЛЬНОЙ спиритуозности!Kotische, 10 Июля 19, 21:48

это не моя проблема. Потому что у меня нет такой прикладной задачи.

Вот это пока не решенная до конца задача, с ПРЕДЕЛЬНОЙ точностью.Kotische, 10 Июля 19, 21:48

А это два раза не моя ситуация.
По первому вопросу я уже доложил, по второму:
чтобы считать результат с предельной точностью, нужно иметь предельно точный измерительный инструментарий.
Манометр и термометр.

У домашнего винокура их нет, и никогда не было.
И не будет.

П.С. Все, что мне нужно было, я неоднократно тебе говорил по телефону, и писал тут и в письмах. Вышел разговор слепого с глухим, потому что, к сожалению, ты оказался неспособен решать практические прикладные задачи.
Это не упрек ни разу, друг мой — просто констатация факта.

Поэтому мы сами сделали программу (довольно тяжелую к сожалению) для показометра, и в макете все работает. Сейчас разводим печатку под регулятор нового поколения, так сказать (с показом Ткип_воды уже в серии)))

П.П.С. Но если случится чудо, и ты родишь несложную формулу определения спиртуозности по Ттекущ и Дтекущ  то с удовольствием вставлю ее в вакуумную автоматику, на которую сейчас пишу ТЗ.
Потому что там оператор при регулировках отбора вообще не будет видеть температуру, а настраивать отбор по спиртуозности, и чем быстрее будет вычисляться последняя, тем точнее будет управление отбором

не нужно пихать в микроконтроллер формулы для всего мысленного диапазона давлений/температур/концентраций. Микроконтроллер вещь специализированная (узкоспециализированная). Загнать в него нехитрый сплайн или полином для нужного узкого диапазона и voi la !Newocelot, 10 Июля 19, 23:34

Вы оба не правы.
Ну ладно 223му простительно, его интересуют только граничные условия области применимости и он упорно не желает смотреть "под капот", что бы разобраться как этого можно достичь.
Но раз ты затронул тему точности - поясню.
Когда ты выражаешь одну велечилу через другую погрешность исходной величины умножается на производную функции в данной точке. Так вот маленькие исходные погрешности могут вырастать в здоровых слонопотамов. Сплайн к сожалению не может уточнить исходные данные, он лишь добавит туда погрешнось. По этому прежде чем строить сплайн нужно подготовить для него данные. Чем меньше шум тем лучше будет работать сплайн.
А шум тем меньше чем больше точек участвуют в усреднении. А усреднять по далеким точкам можно только зная функциональную зависимость лежащую в основе данных. И чем шире диапазон тем больше точек усредняется тем ниже шум, тем лучше будет потом работать с плайн в узком диапазоне.

это не моя проблема. Потому что у меня нет такой прикладной задачи.игорь223, 11 Июля 19, 05:32

Да твоя это проблема, или ты предпологаешь что кроме измерения давления кипящей браги строго 10° спирта больше ничего мерять не надо?
Так в дефлегматоре такие крепости встречаются редко, так что от нуля и до азеатропа область измерения как не крути должна быть.

что кроме измерения давления кипящей браги строго 10° спирта больше ничего мерять не надо?Kotische, 11 Июля 19, 08:00

Кроме измерения давления в ресивере (даже практически всегда не в кубе), с кубовой навалкой неизвестных нам ХХ процентов обьемной крепости, еще измеряется температура кипения куба.
Или дефлегматора.
В обоих случаях приходится считать давления в точках измерения температуры и давления равными

И по этим двум данным вычисляется третья — спиртуозность.
Либо эти ХХ процентов в кубе, либо УУ процентов в дефлегматоре.

Я же говорю, разговор слепого с глухим...

Именно! Потому что давление и температуру надо измерять в одной и той же точке, а не в кубе-температуру, а давление в ресивере.

Измеряй, ктож против.
Я тебе пишу о прикладной реальной задаче, о том что есть, а не о том, что в теории бывает.

А в том, что есть, обычно у термометра от 0.5 до 3 процентов погрешность, у датчика давления от 0.1 до 1 процента.

И хера там твоя формула с погрешностью 0.0001 процента уперлась,
да еще с вычислением обратной величины — давления от спиртуозности, которая вообще никому на практике не известна...и наоборот, только она и интересна винокуру!

хера там твоя формула с погрешностью 0.0001 процента уперласьигорь223, 11 Июля 19, 08:12

Имея запас по погрешности в формуле на которой основывается весь рассчет мы можем проверять и подгонять корректность всех остальных формул.
Ты расстраивался что в алгоритм в микроконтроллер не лезет, так для этого нужно переписать формулу в сплайн, а сплайн по исходным данным построить не получится они слишком шмные, и сплайн получится хреновый.
Так что я именно прикладную инженерную задачу решаю - оцениваю влияние имеющихся погрешностей на практическую реализацию процесса.

Добавлено через 18ч. 20мин.:

Нашел сравнение разных моделей.
Для расчета спирто-водяных смесей лучше всего подходит модель NRTL
Утверждается что точность модели NRTL выше чем модели ВанЛаара.
И для неё я даже нашел статейку со справочными коэфициентами для смеси этанол-вода.
Будем пилить этот алгоритм.

алгоритм в микроконтроллер не лезетKotische, 11 Июля 19, 08:33

а кто мешает в память микроконтроллера забить таблицу ?
входные данные-то весьма дискретны
займёт она там МегаБайт 20 памяти , что по-нынешнему - копейки

а "точные" данные для таблицы вычислить хоть по формуле Пенга-Робинсона, хоть по Парусницу-Ренону, хоть "ПоКотище"



и  для информации http://www.gibbsim.ru/reviews/ModCub.htm

Newocelot, метанол при 50 МПа - это круто!
Осталось только 223го убедить, что для электронного вакуумного попугая нужна именно эта формула

вычислить хоть по формулеNewocelot, 12 Июля 19, 17:27

По любой (более-менее) подходящей

Kotische, быть может, случился какой-то прогресс с волшебной формулой спиртуозности по температуре и давлению? ,)